![]() 综合与实践 测量与误差
综合与实践 测量与误差
1、选择题
1.如图是小明设计用手电来测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A发出经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB丄BD,CD丄BD,且测得AB=1.2米,BP=1.8米,PD=12米,那样该古城墙的高度是()
A.6米 B.8米 C.18米 D.24米

2.如图,A,B两点分别坐落于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够,于是他想了一个方法:在地上取一点C,使它可以直接到达A,B两点,在AC的延长线上取一点D,使![]() ,在BC的延长线上取一点E,使
,在BC的延长线上取一点E,使![]() ,测得DE的长为5米,则A,B两点间的距离为()
,测得DE的长为5米,则A,B两点间的距离为()
A.6米 B.8米 C.10米 D.12米
3.如图是一个照相机成像的示意图,假如底片AB宽40mm,焦距是60mm,所拍摄的2m外的景物的宽CD为()
A.12m B.3m C.![]() D.
D.![]()
2、填空题
4.如图,借助标杆BE测量建筑物的高度.若标杆BE的高为1.5m,测得AB=2m,BC=14m,则楼高CD为______m.
5.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整我们的地方,设法使斜边维持水平,并图27-2-61且边DE与点B在同一直线上.已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=8m,则树高AB=______m.
6.如图,平面直角坐标系的原点O是正方形ABCD的中心,顶点A,B的坐标分别为、 ,把正方形ABCD绕原点O逆时针旋转45°得到正方形A'B'C'D',则正方形ABCD与正方形A'B'C'D'重叠部分形成的正八边形的边长为____.

3、解答卷
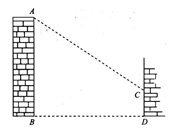
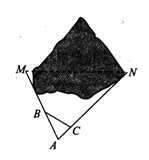
7.小张在课外活动时,发现一个烟囱在墙上的影子CD正好和自己一样高.他测得当时自己在平地上的影子长2.4米,烟囱到墙的距离是7.2米,假如小张的身高是1.6米,你能否据此算出烟囱的高度?
8.当你乘车沿一平坦的大道向前行驶时,你会发现,前方那些高中一年级些的建筑物仿佛“沉”到了坐落于它们前面的矮一些的建筑后面去了。如图,已知楼高AB=18米,CD=9米,BD=15米,在N处的车内小明的视点距地面2米,此时刚好可以看到楼AB的P处,PB恰好为12米,再向前行驶一段距离到F处,从距离地面2米高的视点刚好看不见楼AB,那样车子向前行驶的距离NF为多少米?
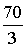
9.如图,M、N为山两侧的两个村庄,为了两村交通便捷,依据国家的惠民政策,政府决定打一直线涵洞.工程职员为了计算工程量,需要计算M、N两点之间的直线距离,选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米、AN=1.8千米,AB=54米、BC=45米、AC=30米,求M、N两点之间的距离.
10.在同一时刻两根木杆在太阳光下的影子如图所示,其中木杆AB=2米,它的影子BC=1.6米,木杆PQ的影子有一部分落在墙上,PM=1.2米,MN=0.8米,求木杆PQ的长度.
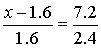
11.如图,A,B两点间有一湖泊,没办法直接测量AB的长,测得CA=60米,CD=24米,DE∥AB,DE=32米.求AB的长.
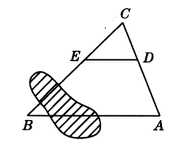
12.如图,A,B两点分别坐落于一个池塘的两端,因为受条件限制没办法直接测量A,B
间的距离.小明借助学过的常识,设计了如下三种测量办法,如图①、②、③所示(图
中a,b,c表示长度).
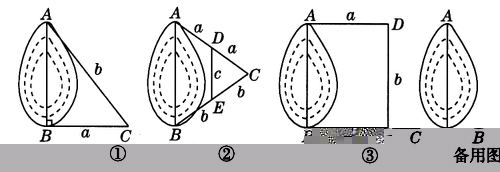
(1)请你写出小明设计的三种测量办法中AB的长度:
图①中,AB=______,图②中,AB=______,图③中,AB=______;
(2)请你再设计一种不同于以上三种的测量办法,画出示意图(不需要写画法),用字母
参考答案
1.B 分析 由反射角等于入射角及等角的余角相等知,∠APB=∠下载成本. 又∠ABP=∠CDP=90°,
∴△ABP∽△CDP,
![]() =8(米).
=8(米).
2. C 分析 ∵在△ABC和△DEC中,![]() ,且∠ACB=∠DCE,∴△ABC∽△DEC,∴
,且∠ACB=∠DCE,∴△ABC∽△DEC,∴![]() .又∵DE=5米,∴AB=10米.
.又∵DE=5米,∴AB=10米.
3. D 分析 ∴AB∥CD,∴△AEB∽△DEC,∴![]() ,即
,即![]() ,∴CD=
,∴CD=![]() m.
m.
注意:本题应该注意单位的统一问题.
4. 12 分析 ∵EB⊥AC, DC⊥AC,∴EB∥DC,
∴△ABE∽△ACD,∴![]()
∵BE=1.5,AB=2,BC=14,
∴AC=16,∴![]() ,∴CD=12.
,∴CD=12.
5. 5.5 分析 ∵∠DEF=∠BCD=90°, ∠D=∠D,
∴△DEF∽△DCB,∴![]() .
.
∵DE=40cm=0.4m,EF=20cm=0.2m,AC=1.5m,CD=8m,
∴![]() ,∴BC=4m,
,∴BC=4m,
∴AB=AC+BC=1.5+4=5.5(m).
6.![]() 分析:如图所示,依据题意可得,A'D'=AB=2,
分析:如图所示,依据题意可得,A'D'=AB=2,![]() ,OM =1,依据△FMD'∽△A'OD',得
,OM =1,依据△FMD'∽△A'OD',得![]() ,即
,即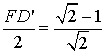 ,则
,则![]() ,则
,则![]() .
.
∴![]() ,即正八边形的边长为
,即正八边形的边长为![]() .
.

7.解:作CE⊥AB于E.
设△MNM'中MN、NM'分别为小张和他的影子.
则△ACE∽△MM'N.
设烟囱高为x米,则![]() ,解得x=6.4.
,解得x=6.4.
所以烟囱高6.4米.
8.解:如下图,∵AB∥CD,∴△ABR∽△CDR,∴![]() ,
,
即![]() ,解得DR=15 .
,解得DR=15 .
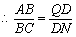
∵CD∥EF,∴△CDR∽△EFR,
∴![]() ,∴
,∴![]() ,
,
解得![]() ,∴
,∴ ![]() .
.
∵PB∥CD,∴△PBT∽△CDT,
∴![]() ,∴
,∴![]() ,解得DT=45 .
,解得DT=45 .
∵AB∥MN,∴△PBT∽△MNT,
∴![]() ,∴
,∴![]() ,解得NT=10,
,解得NT=10,
∴![]() ,
,
∴车子向前行驶的距离NF为![]() 米.
米.
9.解:在△ABC与△AMN中,![]() ,
,![]() ,
,
∴![]() ,∵∠A=∠A,
,∵∠A=∠A,
∴△ABC∽△ANM,
∴![]() ,即
,即![]() ,解得MN=1.5 ,
,解得MN=1.5 ,
因此,M、N两点之间的直线距离是1.5千米.
10. 解:如图,过点N作ND⊥PQ于D,则DN=PM,
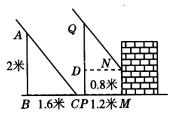
∴△ABC∽△QDN,
![]() .
.
∵AB=2米,BC=1.6米,PM=1.2米,NM=0.8米,
![]() =1.5(米),
=1.5(米),
∴PQ=QD+DP=QD+NM=1.5+0.8=2.3(米).
答:木杆PQ的长度为2.3米.
11. 解:∵DE∥AB,
∴△CDE∽△CAB,∴![]() .
.
又∵CD=24米,CA=60米,DE=32米,
∴![]() ,∴AB=80米,即AB的长是80米.
,∴AB=80米,即AB的长是80米.
12. 解:(1)①![]() ;②2c;③b.
;②2c;③b.
(2)本题办法不少,下面列出3种供参考.
办法1:如图1.

办法2:如图2.
办法3:如图3.







